不围棋

题目背景

「不围棋」是一种非常有趣的棋类游戏。

大家都知道，围棋的「气」是指一个棋子所在的联通块相邻的空格。两粒棋如果在棋盘上线段的两端就认为是相邻的，也就是在同一个连通块里。比如在图中，白子为四个独立的连通块，黑子构成一个连通块，绿色点是黑子连通块唯一的「气」：

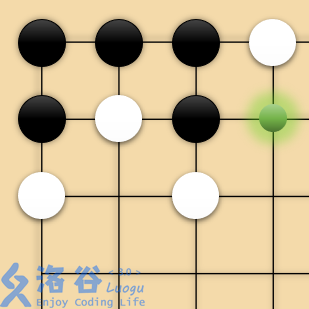
「提子」是指将没有「气」的棋子提出棋盘，在上图中，如果白方走绿点，那么就可以将黑子全部提走。

在围棋中，我们想尽量多地占领地盘、提走对方棋子。然而，不围棋恰恰相反——不围棋是一种非常和平的游戏，双方的走子不能产生任何提子，也就是说，任何一次走子不能让棋盘上任何一个棋子所在的连通块没有气。比如，白方在上图中不能走绿点。

在你的某一步棋后，对方无棋可走，那么你就赢了。

题目描述

小 F 对不围棋特别感兴趣，不过他经常输，所以他想做出一个 AI 来替他完成这局游戏。

不过造 AI 实在是太困难啦，小 F 千辛万苦写出来的 AI 被同学们的 AI 锤爆啦！

现在，他想请你帮他实现一个 AI 中一部分的功能——随机模拟，因为他相信你写的程序非常优秀，一定能优化他的 AI。

给你一个 $n \times n$ 的棋盘，上面或许已经有一些棋子了，但此时局面一定是合法的，即不存在没有气的连通块；此时轮到黑棋下棋，因此棋盘上黑白棋子的数量一定是相等的。

你的任务是，依次为黑棋和白棋随意指定一个可行的走子位置，直到某一步游戏无法进行，决出胜负为止。

在正式的不围棋比赛还存在一些禁手规则。不过由于小 F 玩的是一种棋盘大小可变的新型不围棋，我们只用考虑上面提到的气的规则就好。

输入格式

输入一行一个整数 $n$，表示棋盘大小。 输入接下来 $n$ 行，每行有一个长度为 $n$ 的字符串，表示第 $i$ 行的情况。

• . 表示空
• X 表示黑棋
• O 表示白棋

详细请参考样例。

输入保证，棋盘初始局面合法，X 与 O 数量相等。

输出格式

你需要输出至少一行，假设你输出了 $L$ 行，那么对于前 $L - 1$ 行，你应该输出两个用空格分隔的正整数表示下棋坐标 $x_i, y_i$，其中奇数行表示黑棋的行动，偶数行表示白棋的行动。$x$ 坐标为从上到下从 $1$ 到 $n$，$y$ 坐标为从左到右从 $1$ 到 $n$。

请在第 $L$ 行输出 -1 -1，表示此时第 $L$ 手执棋人已经无棋可走。

你的输出可能会很大，即使本题时限为 $3s$，也请你不要使用太慢的方法输出大量内容。

评分方式：

本题启用 Special Judge，并且有部分分。我们将通过以下方式进行计分：

• 如果你输出格式错误，那么该测试点不得分。格式错误包括但不限于：输出了非数字内容；一行输出了超过或者少于两个正整数；输出的坐标在棋盘外；最后一行的输出不是 -1 -1。
• 如果你的输出格式正确，但是你的输出的第一行的答案就是不可接受的，那么该测试点不得分。例如：输出的坐标是黑棋不可以下的位置；黑棋有棋可走却输出了 -1 -1。
• 如果你的输出格式正确，并且你的前 $k(1 \leq k <L)$ 行输出是可以接受的，那么该测试点将至少得到 $s$ 分，其中 $s = \lfloor \lg k \rfloor + 1$，含义是 $k$ 在十进制表示下是一个 $s$ 位数。
• 如果你的输出完全正确，无论你输出了多少行，你都将得到 $10$ 分。

详情请参考样例解释。

样例 #1

样例输入 #1

3
XXX
OOX
OO.

样例输出 #1

-1 -1

样例 #2

样例输入 #2

3
XOO
XO.
X..

样例输出 #2

2 3
-1 -1

提示

样例 1 解释：

注意到将棋盘下满会让棋盘上所有连通块都没有气，所以黑棋是无棋可走的。

样例 2 解释：

样例 2 还有两个正确的输出是这样的：

3 2
2 3
-1 -1

3 3
2 3
-1 -1

我们将棋盘表示出来：

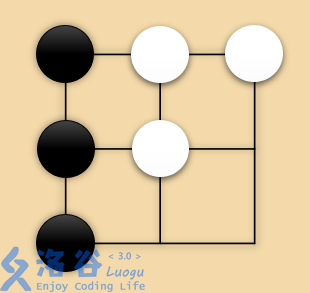
其中，黑棋是三个空格都可以走的。

• 如果黑棋走 $(2, 3)$，如图，此时白棋走任何位置都会提走相邻的黑棋，白棋无棋可走；
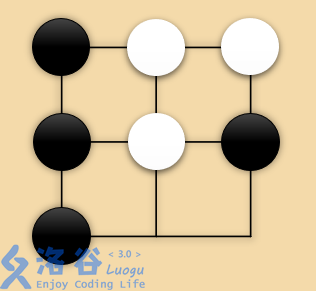
• 如果黑棋走 $(3, 2)$，如图，此时白棋唯一可走的点是 $(2, 3)$，之后黑棋无棋可走；
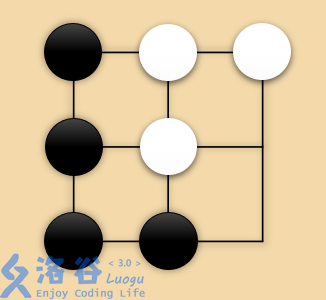
• 如果黑棋走 $(3, 3)$，如图，此时白棋唯一可走的点是 $(2, 3)$，之后黑棋无棋可走；

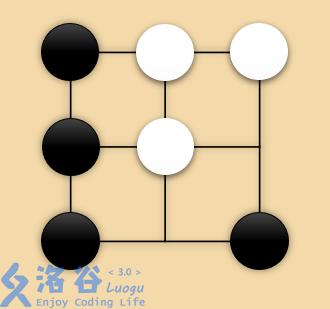
这三种情况依次对应三个输出，输出任意一种可得到满分。

评分规则解释：

为了解释评分规则，我们以样例 2 为例，对于以下几种输出：

I AK IOI

很不幸，因为您太强了，所以为了按住躁动的您，我们会给您 $0$ 分。

-1 -1

1 1
-1 -1

很不幸，你的第一行没有输出正确，得 $0$ 分。

3 3
-1 -1

你输出的前 $1$ 行是正确方案的一部分。由于 $1$ 是 $1$ 位数，恭喜你得到了整整 $1$ 分！

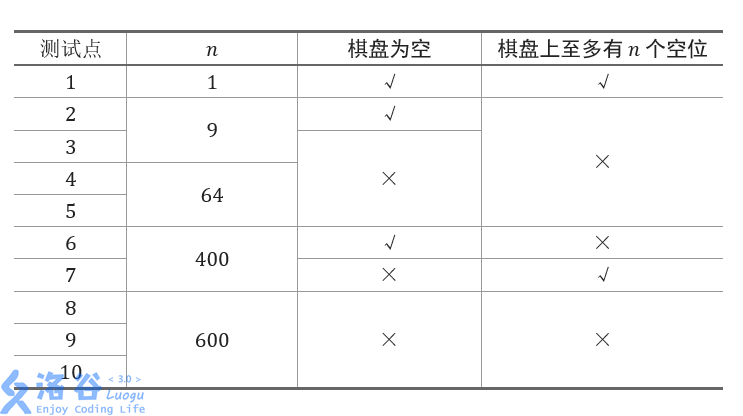
数据范围：